如果你是NLP领域初学者，欢迎关注我的博客，我不仅会分享理论知识，更会通过实例和实用技巧帮助你迅速入门。我的目标是让每个初学者都能轻松理解复杂的NLP概念，并在实践中掌握这一领域的核心技能。
通过我的博客，你将了解到：

  • NLP的基础概念，为你打下坚实的学科基础。
  • 实际项目中的应用案例，让你更好地理解NLP技术在现实生活中的应用。
  • 学习和成长的资源，助你在NLP领域迅速提升自己。

不论你是刚刚踏入NLP的大门，还是这个领域的资深专家，我的博客都将为你提供有益的信息。一起探索语言的边界，迎接未知的挑战，让我们共同在NLP的海洋中畅游！期待与你一同成长，感谢你的关注和支持。欢迎任何人前来讨论问题。

【NLP基础知识三】词嵌入（Word Embeddings）之“GloVe：单词表示的全局向量”

4、Word2Vec：一种基于预测的方法

核心思想

让我们再次回顾一下核心思想：

核心思想：我们需要将有关上下文的信息引入词向量中。

虽然基于计数的方法直观地实现了这个想法，但 Word2Vec 以不同的方式实现它：

方法：通过预测上下文来学习好的词向量。
Learn word vectors by teaching them to predict contexts.

Word2Vec 是一个参数是词向量的模型。这些参数针对某个目标进行迭代优化。而该优化目标迫使词向量“知道”一个词可能出现的上下文：训练向量来预测相应词可能的上下文。正如在分布假设中所说的，如果向量“知道”了上下文，它们就能“知道”单词的含义。
2024-01-27T16:04:30.png
Word2Vec 是一种迭代方法。其核心思想如下：

  • 首先，先找一个巨大的文本语料库；
  • 接着，使用滑动窗口浏览文本，每次移动一个单词。在每一步时，都会有一个中心词(Central Word)和上下文词（Context Words, 即同一窗口中的其他词）；
  • 然后，计算上下文词在以此中心词作为条件下出现的概率；
  • 最后，优化中心词向量以增加上述概率。

2024-01-27T16:05:55.png
2024-01-27T16:06:09.png
2024-01-27T16:06:20.png
2024-01-27T16:06:27.png
2024-01-27T16:06:36.png
2024-01-27T16:06:45.png

目标函数：负对数似然

对于文本语料库中的每个位置$t =1, \dots, T$，Word2Vec 在给定中心词的 m 大小窗口内预测上下文词$w_t$：

$$ \color{#88bd33}{\mbox{Likelihood}} \color{black}= L(\theta)=\prod\limits_{t=1}^T\prod\limits_{-m\le j \le m, j\neq0}P(\color{#888}{w_{t+j}}|\color{#88bd33}{w_t}\color{black}, \theta), $$

$θ$ 是需要被优化的参数（即词向量）。 目标函数（又名损失函数或成本函数） $Jθ$ 则是平均负对数似然：
2024-01-28T05:05:38.png
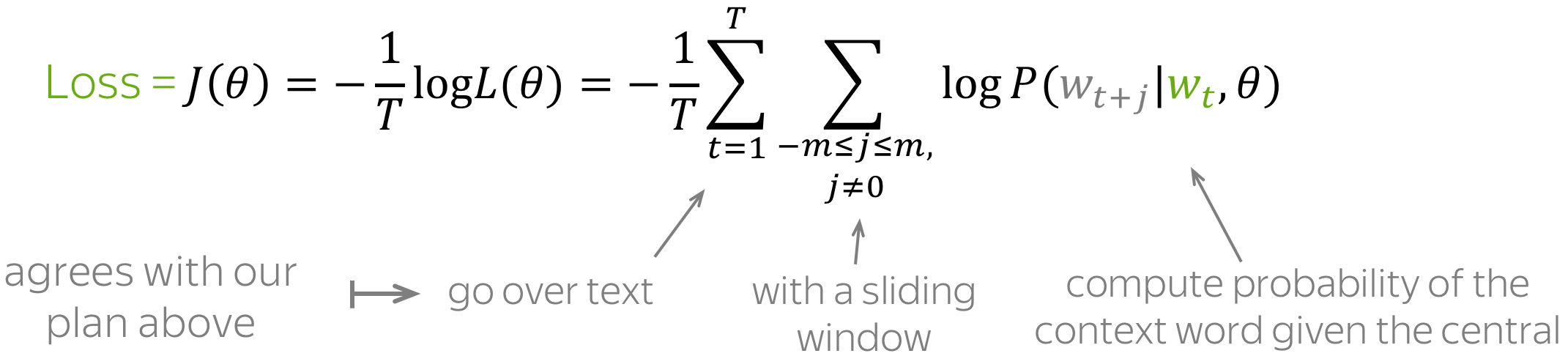
请注意损失与上面核心思想的吻合程度：使用滑动窗口浏览文本并计算概率。 现在让我们来看看该如何计算这些概率。

如何计算 $P(\color{#888}{w_{t+j}}\color{black}|\color{#88bd33}{w_t}\color{black},\theta)?$

2024-01-28T05:08:57.png
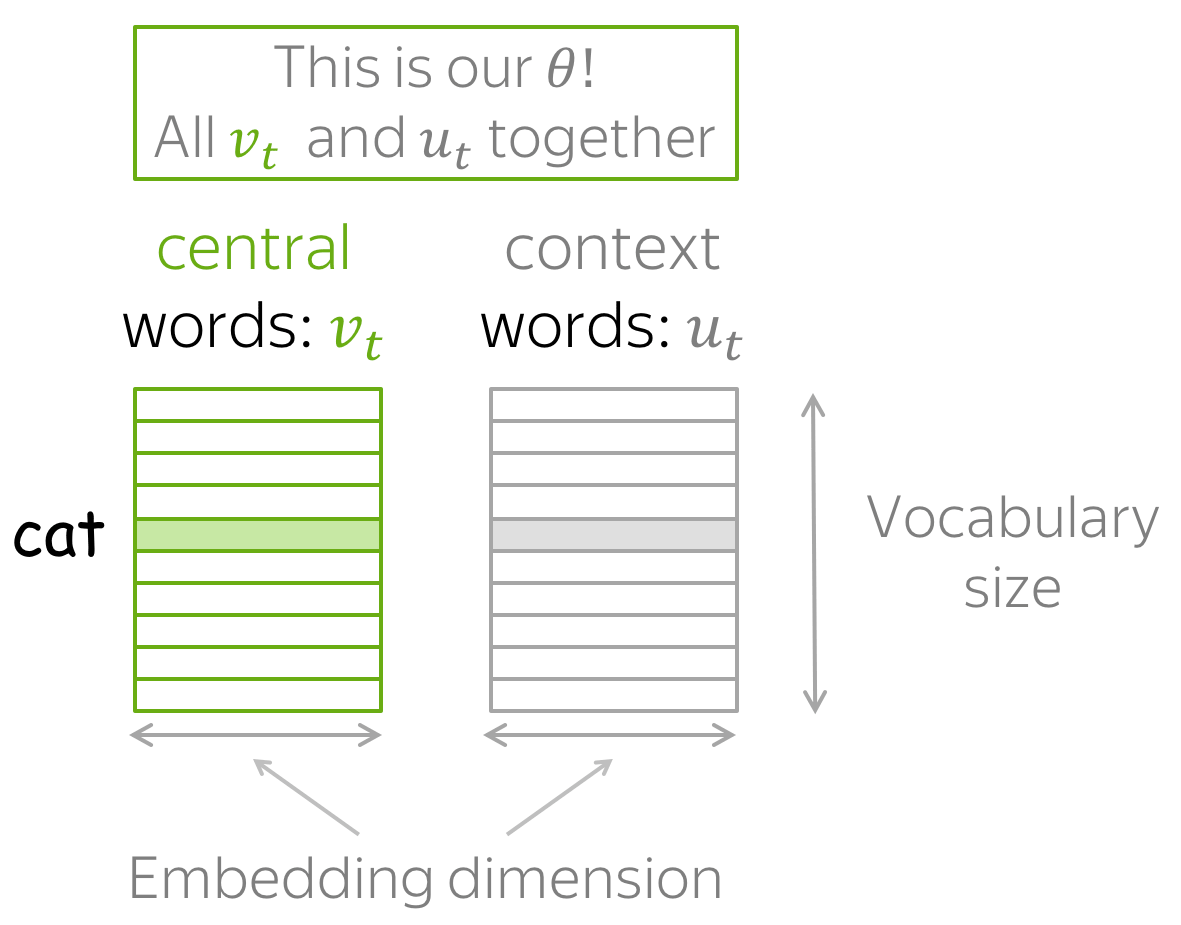
对于每个单词 $w$ 我们有两个向量：

  • 当它是一个中心词时，用$v_w$ 表示该词
  • 当它是一个上下文词时，用$u_w$ 表示该词

（在训练结束后，我们通常会丢弃上下文词向量，仅使用中心词向量作为一个词的向量表征。）
于是，对于中心词 $c$ 和 上下文词 $o$，，上下文词在该中心词的窗口中出现的概率是：
2024-01-28T05:10:51.png
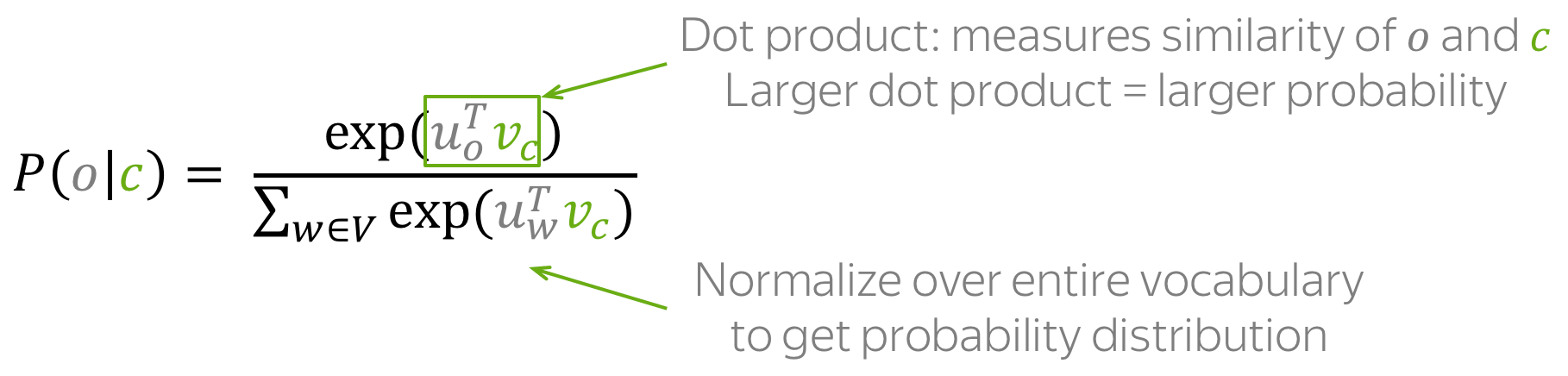
注意：上式实际上就是softmax函数！

$$ softmax(x_i)=\frac{\exp(x_i)}{\sum\limits_{j=i}^n\exp(x_j)}. $$

softmax 会映射任意值 $x_i$ 到概率分布 $p_i$:

  • "max" 因为最大的 $x_i$ 将有最大的概率 $p_i$;
  • "soft" 因为所有概率都不为零。

您将在自然语言（以及一般的深度学习）课程中大量地使用到此函数。
2024-01-28T05:18:03.png
2024-01-28T05:18:14.png
2024-01-28T05:18:23.png
2024-01-28T05:18:32.png
2024-01-28T05:18:41.png
2024-01-28T05:18:49.png

如何训练：梯度下降, 一次一词

让我们回想一下，对于词汇表中的任一单词，Word2Vec 模型的参数 $\theta$ 都有两个向量对应，分别是向量 $\color{#88bd33}{v_w}$ 和 $\color{#888}{u_w}$。 这些向量可以通过梯度下降优化训练目标来学习（需要指定学习率 $\alpha$)：

$$ \theta^{new} = \theta^{old} - \alpha \nabla_{\theta} J(\theta). $$

一次一词

每一次模型优化时，我们都会更新一次模型参数，而每次更新都只针对一个中心词和它的一个上下文词。回顾一下损失函数：

$$ \color{#88bd33}{\mbox{Loss}}\color{black} =J(\theta)= -\frac{1}{T}\log L(\theta)=-\frac{1}{T}\sum\limits_{t=1}^T\sum\limits_{-m\le j \le m, j\neq 0}\logP(\color{#888}{w_{t+j}}\color{black}|\color{#88bd33}{w_t}\color{black},\theta)=\frac{1}{T}\sum\limits_{t=1}^T\sum\limits_{-m\le j \le m, j\neq 0} J_{t,j}(\theta). $$

对于中心词 $\color{#88bd33}{w_t}$, 每个上下文词损失函数中都包含项$J_{t,j}(\theta)=-\logP(\color{#888}{w_{t+j}}\color{black}|\color{#88bd33}{w_t}\color{black},\theta)$. 仔细看一下这一项，就可以知道该如何对此步骤进行更新。举个例子，假设我们有一个句子
2024-01-28T05:23:47.png
这个句子里明显可以看到有一个中心词 cat 和四个上下文词 cute, grey, playing 和 in。 由于一次只看一个词，我们将只选择一个上下文词，下面将以 cute 为例。 那么仅包含中心词 cat 和上下文词 cute 的损失项即可写成：

$$ J_{t,j}(\theta)= -\log P(\color{#888}{cute}\color{black}|\color{#88bd33}{cat}\color{black}) = -\log \frac{\exp\color{#888}{u_{cute}^T}\color{#88bd33}{v_{cat}}}{ \sum\limits_{w\in Voc}\exp{\color{#888}{u_w^T}\color{#88bd33}{v_{cat}} }} = -\color{#888}{u_{cute}^T}\color{#88bd33}{v_{cat}}\color{black} + \log \sum\limits_{w\in Voc}\exp{\color{#888}{u_w^T}\color{#88bd33}{v_{cat}}}\color{black}{.} $$

此步骤中，哪些参数会被更新呢？

  • 中心词向量中，被更新的仅有 $\color{#88bd33}{v_{cat}}$;
  • 上下文词向量中，词汇表中所有单词的表示 $\color{#888}{u_w}$ 都会被更新。

下面是此步骤推导的示意图。
2024-01-28T05:25:32.png
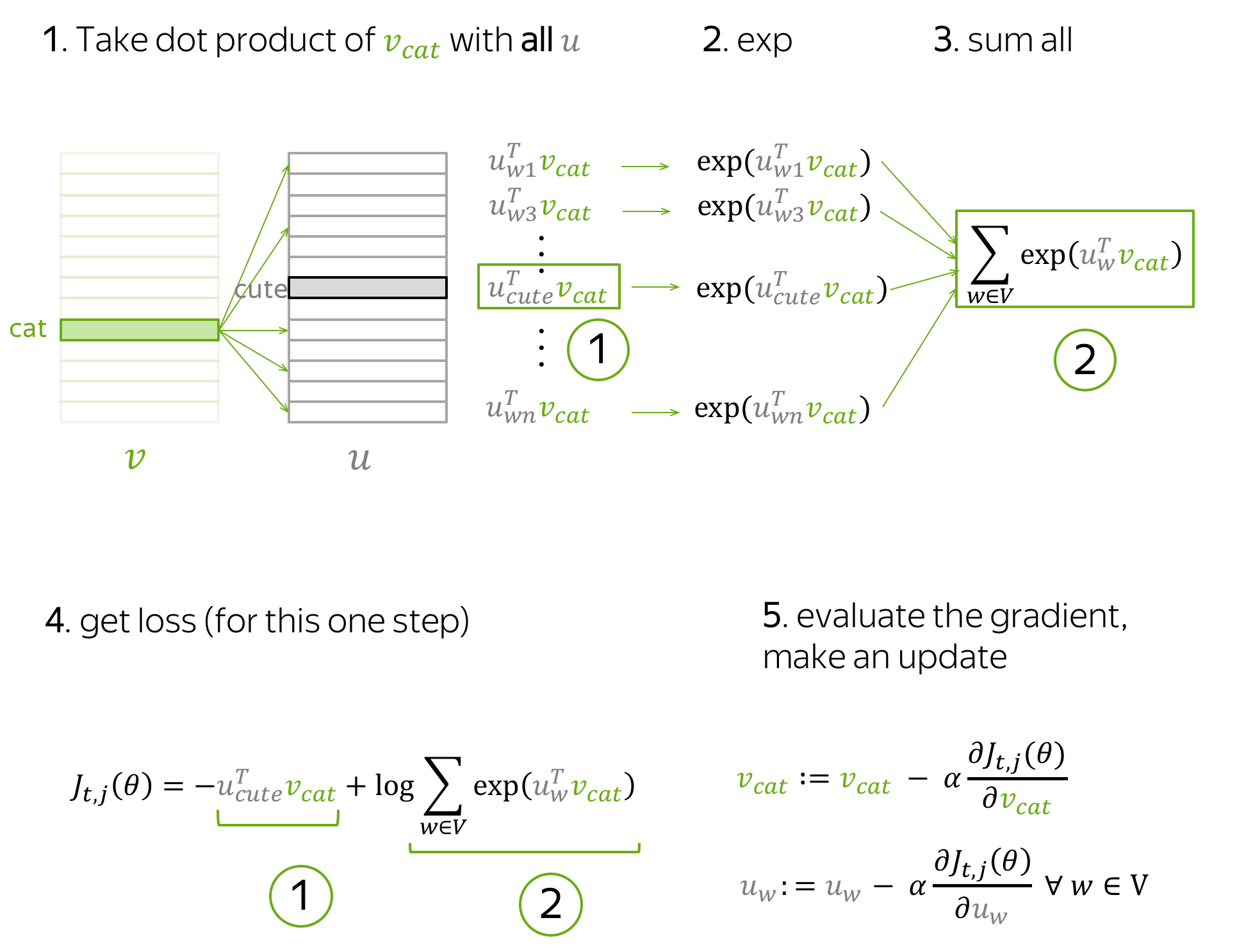
直观地，上述公式过程会通过参数更新以最小化 $J_{t,j}(\theta)$，本次更新可以让 $\color{#88bd33}{v_{cat}}$ 和 $\color{#888}{u_{cute}}$ 变得更相似（点积意义上的），并同时降低 $\color{#88bd33}{v_{cat}}$ 和词汇表内所有其他单词 $\color{#888}{u_{w}}$的相似度。
这听起来可能有点奇怪：如果其他词中也包含有效的上下文词（例如，示例句中的 grey, playing 和 in），为什么我们要降低$\color{#88bd33}{v_{cat}}$和所有其它单词之间的相似性？
别担心：因为我们会更新每个上下文词（当然还有所有中心词），平均下来我们的词向量将学习到所有可能上下文的分布，即意味着本次对有效上下文词的降低会在其他的样例中被补偿。

更快的训练：负采样

在上面的示例中，对于每对中心词及其上下文词组成的训练样本，我们必须更新所有上下文词的向量。这无疑是非常低效的，因为每一步进行更新所需时间与总的词汇表大小成正比。
但是，为什么我们必须在每一步都考虑词汇表中所有上下文词的向量呢？假设还是在刚才的示例中，我们考虑的并不是所有上下文单词的向量，而是只有目标上下文词（cute）和几个随机选择的其他单词，就像下图：
2024-01-28T05:27:34.png
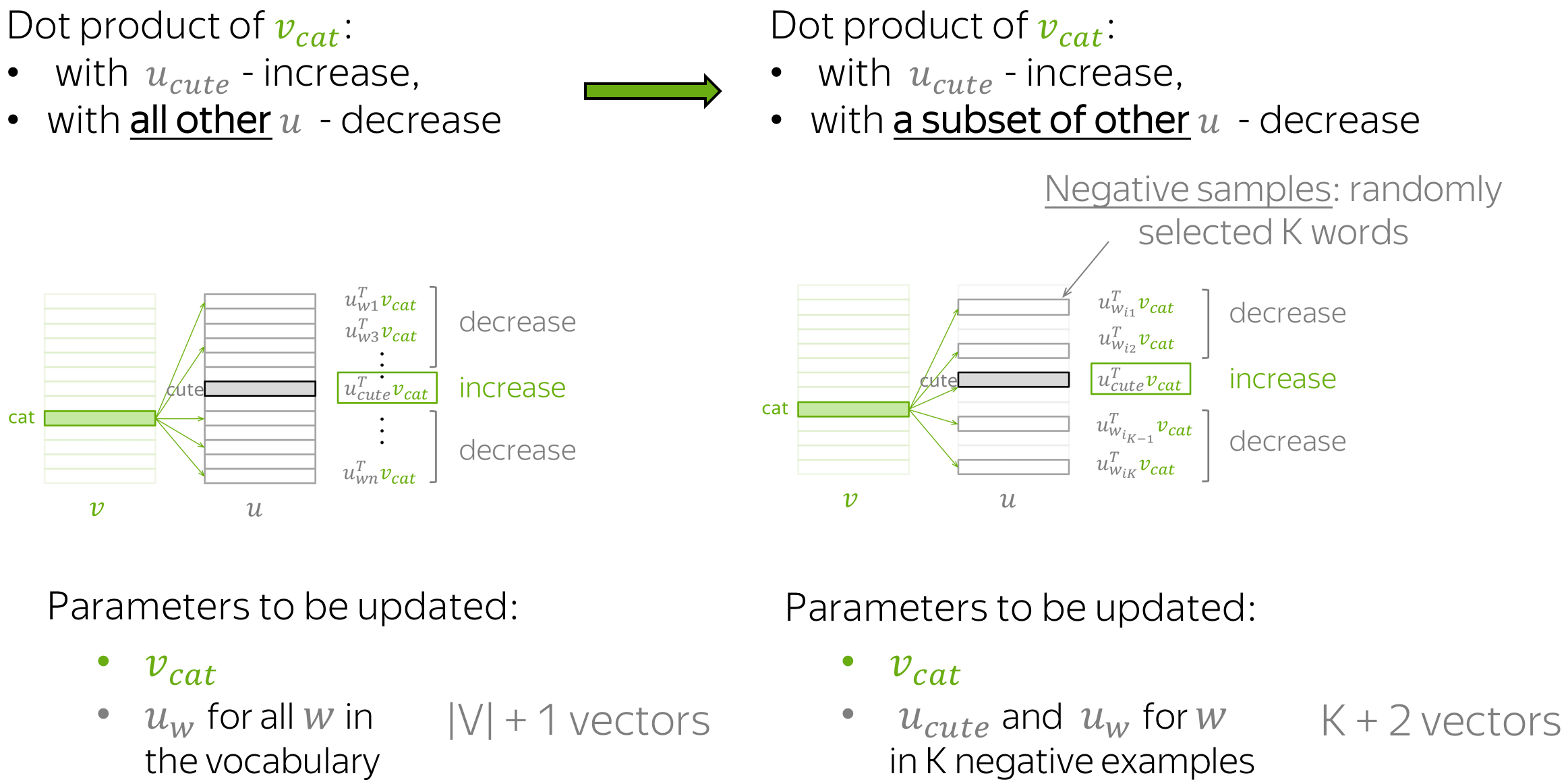
和以前一样，参数的更新增加了 $\color{#88bd33}{v_{cat}}$ 和 $\color{#888}{u_{cute}}$ 两者之间的相似性。 不同的是，现在我们只降低了 $\color{#88bd33}{v_{cat}}$与K 个负样本子集单词上下文向量的相似性，而非所有单词。
由于我们有一个庞大的语料库，平均下来我们将更新每个向量足够的次数，并且向量仍然能够很好地学习单词之间的关系。
正式地，此步骤的新损失函数即：

$$ J_{t,j}(\theta)= -\log\sigma(\color{#888}{u_{cute}^T}\color{#88bd33}{v_{cat}}\color{black}) - \sum\limits_{w\in \{w_{i_1},\dots, w_{i_K}\}}\log\sigma({-\color{#888}{u_w^T}\color{#88bd33}{v_{cat}}}\color{black}), $$

$w_{i_1},\dots, w_{i_K}$ 是这一步的K个负样本 ，$\sigma(x)=\frac{1}{1+e^{-x}}$ 是sigmoid激活函数.
注意， $\sigma(-x)=\frac{1}{1+e^{x}}=\frac{1\cdot e^{-x}}{(1+e^{x})\cdot e^{-x}} =

                        \frac{e^{-x}}{1+e^{-x}}= 1- \frac{1}{1+e^{x}}=1-\sigma(x)$. 于是loss函数可以被写成：

$$ J_{t,j}(\theta)= -\log\sigma(\color{#888}{u_{cute}^T}\color{#88bd33}{v_{cat}}\color{black}) - \sum\limits_{w\in \{w_{i_1},\dots, w_{i_K}\}}\log(1-\sigma({\color{#888}{u_w^T}\color{#88bd33}{v_{cat}}}\color{black})). $$

负样本的选择

每个单词只有少数“真正”的上下文。因此，随机选择的词大概率是“否定的”，即不是真正的上下文。这个简单的想法不仅可以有效地训练 Word2Vec，还可以用于许多其他应用中，其中一些我们将在后面的课程中看到。
一般地，Word2Vec 根据词的先验分布随机抽取负样本。 假设 $U(w)$ 是单词出现的概率分布, 一般可以用单词在文本语料库中的频率近似计算。Word2Vec 修改了这个分布以更频繁地采样到频率较低的单词，最终它选择 $U^{3/4}(w)$ 进行负样本单词的采样.

Word2Vec 变体：Skip-Gram 和 CBOW

Word2Vec 有两种变体：Skip-Gram 和 CBOW。
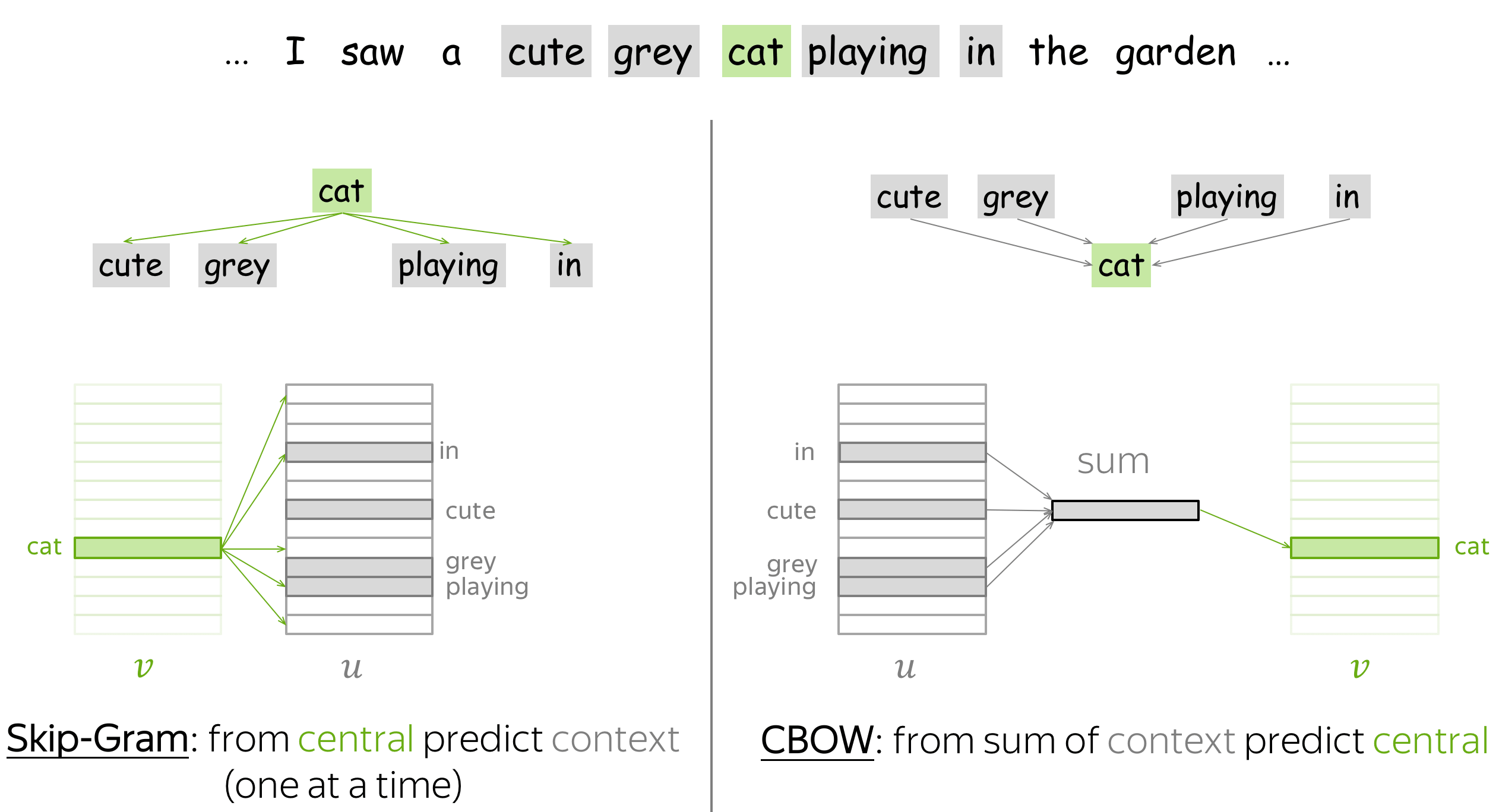
Skip-Gram 就是上文所介绍的模型：给定中心词，预测上下文词。目前，带有负采样的 Skip-Gram 是最流行的方法。
CBOW（Continuous Bag-of-Words，连续词袋模型）则反其道而行之：给定上下文词，预测中心词。 一般来说 CBOW 直接使用上下文词向量的加和来预测，这个加和后的向量也被称为“词袋”。
2024-01-28T05:30:51.png

附加笔记

原始 Word2Vec 论文是这两篇：

你可以通过阅读原文以获取有关实验、实现和超参数的详细信息。本文将提供一些你需要知道的最重要的事。

这并非一个全新的idea (英文原文)

请注意，学习词向量（分布式表示）的想法并不新鲜。例如，有人尝试将词向量作为更大网络的一部分来学习，然后提取出模型的嵌入层作为词向量。有关前人方法的相关信息，可以通过阅读 Word2Vec 原论文摘要获取。

Word2Vec 让人出乎意料的是，它能够在庞大的数据集和大型词汇表上非常快地学习到高质量的词向量。 当然，我们将在分析与解释部分所要介绍的一些有趣的属性让 Word2Vec 闻名遐迩。

为什么要设计两个向量？ (英文原文)

正如上文所介绍的，在 Word2Vec 中，我们要为每个单词训练两个向量：一个是中心词向量，另一个是上下文词向量。 训练后，上下文词向量就被丢掉了。

那既然训练后只用到中心词向量，为什么训练的时候要搞两个向量呢？其实，这正是使 Word2Vec 如此简洁的重要技巧之一！回顾一下损失函数：

$$ J_{t,j}(\theta)= -\color{#888}{u_{cute}^T}\color{#88bd33}{v_{cat}}\color{black} - \log \sum\limits_{w\in V}\exp{\color{#888}{u_w^T}\color{#88bd33}{v_{cat}}}\color{black}{.} $$

当每个单词使用不同的向量来分别表示其作为中心词和上下文词的表征时，损失函数的第一项和指数内的点积对于参数都是线性的（因为两项互不相关）。因此，梯度的计算将异常容易。

关于词嵌入（Word Embeddings）的课程到此结束，如果有什么不明白或者看不懂的地方，以及文章中的错误，欢迎评论。

在这个充满科技魔力的时代，自然语言处理（NLP）正如一颗璀璨的明星般照亮我们的数字世界。当我们涉足NLP的浩瀚宇宙，仿佛开启了一场语言的奇幻冒险。正如亚历克斯·康普顿所言：“语言是我们思想的工具，而NLP则是赋予语言新生命的魔法。”这篇博客将引领你走进NLP前沿，发现语言与技术的交汇点，探寻其中的无尽可能。不论你是刚刚踏入NLP的大门，还是这个领域的资深专家，我的博客都将为你提供有益的信息。一起探索语言的边界，迎接未知的挑战，让我们共同在NLP的海洋中畅游！期待与你一同成长，感谢你的关注和支持。欢迎任何人前来讨论问题。